リプチンスキー定理の数値例

12月20日の講義で述べたリプチンスキー定理について、具体的な数値例を使って示してみます。

第1財を労働集約財、第2財を資本集約財と仮定して、各財の労働投入係数と資本投入係数が下表のようになっていたと仮定する。

このとき、ある国の労働賦存量と資本賦存量をそれぞれ100単位とする。第1財の生産量をx、第2財の生産量をyとすると、第1財の生産に投入されている労働量は労働投入係数3×生産量x＝3x、第2財の生産に投入されている労働量は労働投入係数2×生産量y=2yとなる。両財の生産に投入されている労働量は、この国の労働賦存量100に等しくなるため、3x＋2y＝100が成立していることになる。この式を労働の完全雇用条件と呼ぶ。
同様に、資本については、第1財の生産に投入される資本量が2x、第2財の生産に投入される資本量が3yとなるため、資本の完全雇用条件は2x＋3y＝100となる。これをまとめると次のようになる。

労働の完全雇用条件　3x+2y=100
資本の完全雇用条件　2x+3y=100

これをxとyについて解くと、x＝20，y＝20となる。
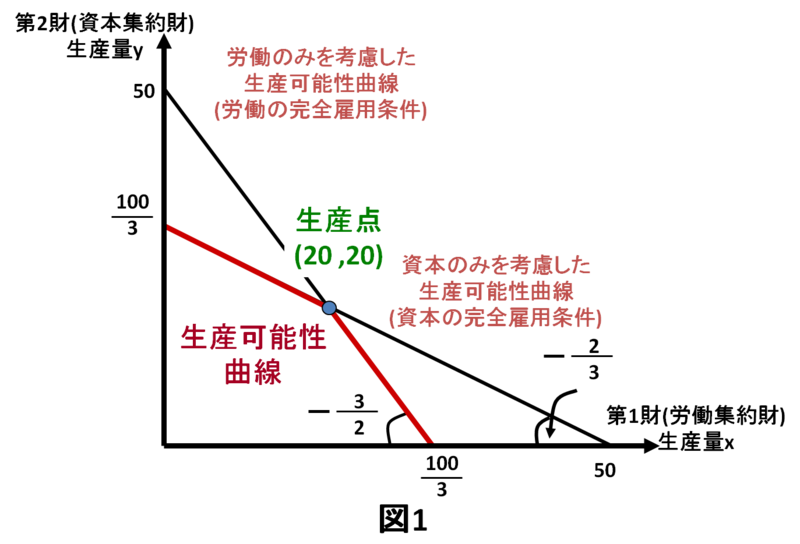
このことを示したものが図1である。講義で述べた労働のみを考慮した生産可能性曲線は労働の完全雇用条件をグラフ化したものであり、資本のみを考慮した生産可能性曲線は資本の完全雇用条件を図示したものであり、その交点が生産点となる。

この状態から、労働賦存量が10単位増加すると考えよう。このとき、労働と資本の完全雇用条件は次のようになる。

労働の完全雇用条件　3x+2y=110
資本の完全雇用条件　2x+3y=100

これを解くと、x＝26，y＝16となり、労働賦存量の増加によって労働集約財の生産量が増加し、資本集約財の生産量が減少するというリプチンスキー定理が成立することが分かる。

労働賦存量が10単位増加し、労働集約財の生産量を増加させようと思っても、労働だけでは労働集約財の生産を行うことはできず、資本をどこかから調達しなければならない。資本集約財の生産を4単位減少すると、資本12単位と労働8単位を労働集約財の生産に投入することが可能となる。これと10単位の労働賦存量の増加を加えると、資本12単位と労働18単位を労働集約財の投入に可能となり、労働集約財の労働投入係数が3、資本投入係数が2であることから、労働集約財の生産は6単位増加することが可能となる。このため、資本集約財の生産量は労働賦存量が増加する前の20単位から4単位減って16単位に、労働集約財の生産量は労働量増加前の20単位から6単位増えて26単位となるのである。
このような労働賦存量の増加が引き起こす産業間の労働・資本の移動を示したものが下図である。

今日はこの辺で